주재걸 교수님의 <인공지능을 위한 선형대수 - 고유값 분해와 선형변화> 강의와 기타 교재를 참고하여 정리하였습니다.
[LECTURE] 고유값 분해와 선형변환 : edwith
학습목표 드디어 이번 강의에서는 이제까지 우리가 배워온 개념을 토대로 고유값 분해에 대해 배워보겠습니다. 그리고 고유값 분해를 통한 선형변환의 과정을 다루겠습니다. 핵심 키워드... - 커넥트재단
www.edwith.org
고유값 분해 (Eigendecomposition)
𝑉𝐷 = 𝐴𝑉
• If 𝐴 is diagonalizable, we can write 𝐷 = 𝑉^(−1)𝐴𝑉.
-> 대각행렬을 만들 수 있다는 것은 역행렬이 존재하다. 따라서 아래와 같은 식도 만들 수 있다.
• We can also write 𝐴 = 𝑉𝐷𝑉^(-1).
which we call eigendecomposition of 𝐴.(=QR decomposition)
• 𝐴 being diagonalizable is equivalent to 𝐴 having eigendecomposition (고유값분해).

QR 분해(decomposition) 처럼 주어진 매트릭스를 여러 개의 곱으로 나타내되, 𝑉와 𝐷 각각의 매트릭스가 조건을 만족해야 한다.
(1) 𝑉는 역행렬(invertable matrix)가 존재해야 하며, (2) 𝐷는 대각 행렬(diagonal matrix)이 가운데에 낀 형태이며, 양쪽에 𝑉, 𝑉^(-1)을 곱하면 오리지널 매트릭스로 복원이되어야 한다. 이를 eigendecomposition이라고 한다.
Linear Transformation via Eigendecomposition

𝐴 행렬은 대각화가 가능하다면, 𝐴 = 𝑉𝐷𝑉^(-1) 으로 고유값 분해(eigendecomposition) 할 수 있다.
𝑇 (x) = 𝐴x 으로 선형변환 한다면, 𝑉 (𝐷 (𝑉^(-1) x) ) 이 된다.

왼쪽 행렬은 고유벡터이기 때문에 효율적인 계산(=각각의 고유값 4, -1 으로 변환)할 수 있다. 그 결과 각 행렬에 고유값을 곱하는 것과 같은 결과인 [4, 8] + [-2, -3] 으로 변환하는 것과 같다.
즉 계산을 빠르게 하기 위해, 어떤 벡터든지 고유벡터(eigenvector)들의 선형결합으로 표현을 하고, 각각 벡터와 그 값을 곱한 걸 나중에 합치는 과정(=eigen decomposition)을 살펴보고자 한다.
Decomposition (1) Change of Basis (기저 변환)
2차원 공간을 생각할 때 {[1, 0], [0, 1]} 등 여러 개의 기저(basis)가 있다. 입력벡터가 [5, 7]인 경우, 간단한 벡터의 선형 결합에 가중치(5 또는 7)를 더한 5 [1, 0] + 7 [0,1] 으로 생각할 수 있다.
5 [1, 0] + 7 [0,1] = a[2, 1] + b[1, 5]
(위 벡터는 컬럼벡터이다)
일 때, a[2, 1] + b[1, 5] 에서 a, b 가 해당하는 값을 구하는 게 기저변환 (change of basis)이다.
a = -1, b = 3 은 a는 (-1)배인 방향만 반대로 바뀌게 되며 b는 3배 만큼 벡터 길이가 늘어난다.

주어진 입력벡터 x = (4,3)의 basis를 새로운 basis로 표현한다면, v1는 2배 늘어나므로 계수 값이 v1=2, v2=1이 된다.
[ 4, 3 ] = 2 [3, 1] + 1 [-2, 1]

동일한 점을 새로운 기저(basis)로 표현하고자 한다. 두 개의 새로운 벡터가 v1, v2 라고 하자. 평행사변형을 이루어 꼭지점 x (4,3) 을 이루고자 한다면 노란색 벡터로 만들 수 있다. v1의 계수값은 두 배를 늘렸으므로 2가 되고, v2는 그대로이기 때문에 1이 된다. 이 과정을 통해서 기저를 변환해 보았다.
이 과정을 식으로 표현한다면 아래 그림 상단에 적힌 식과 같다.
우리가 구해야하는 값은 계수 2와 1이다. 이 값을 구하는 과정을 살펴보면, 주어진 벡터 x [4, 3] 는 컬럼들을 모아서 {[3, 1] [-2, 1]}으로 만들 수 있다. 그 다음 우리가 구해야 하는 값 [2, 1]은 x1, x2 (linear combination의 계수)가 된다.
{[3, 1] [-2, 1]}이 정사각 행렬이며 역행렬이 존재한다고 한다면, 이 행렬을 𝑉라고 한다. 그렇다면 𝑉^(-1) * [4, 3]은 [x1, x2]가 된다.
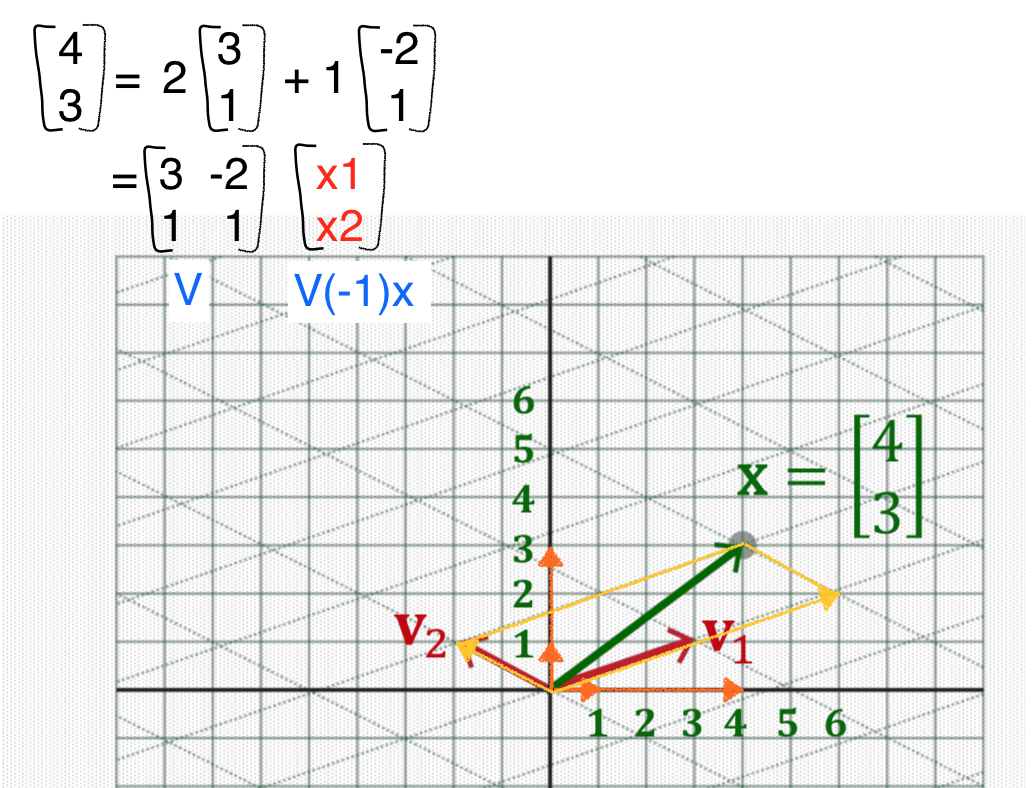
𝐴x = B 를 푼다는 것은 주어진 행렬에서 컬럼벡터의 평행사변형 길이를 맞추는 작업이라고 생각할 수 있다.
변형되는 평행사변형 길이의 배수는 𝑉^(-1)x (=입력벡터) 값이 된다.
𝑉가 역행렬이 존재하지 않을 수 있지만, 처음에 시작할 때 𝐴는 diagonalizable 하므로, n차원에서 n개의 선형독립하는 벡터를 찾을 수 있다. 따라서 정사각행렬이고, 선형독립이기 때문에 𝑉의 역행렬이 존재할 수밖에 없다.
Ax를 일련의 세 번의 변환으로 봤을 때, 첫 번째 변환인 𝑉^(-1)x 은 고유벡터를 기저(v1, v2)로 삼은 뒤 선형결합의 계수 값을 구하는 과정이다.

Decomposition (2) Element-wise Scaling
두 번째 변환은 대각행렬 𝐷와 곱하는 과정이다.

대각행렬 𝐷와 벡터의 곱은 element끼리만 곱하면 되기 때문에 계산이 간단하다. 이는 행렬이 아닌 고유값(eigenvalue)인 상수 𝜆 와 백터를 곱했을 때 계산이 간단해지는 역할을 대각화에서도 살펴볼 수 있다.

[2, 1]은 고유벡터들의 선형결합에 해당하는 coeifficient가 된다. 단순하게 몇 배로 해주는지는 고유값(eigenvalue) [-1, 2]를 곱하면 된다.
즉, 𝐴 를 곱할 때 벡트의 길이와 방향을 바꾸는 역할을 했는데, 두 개의 고유벡터들의 선형결합에 𝐴를 곱해도 크기는 바뀌어도 방향은 그대로 유지된다. 크기만 바꾸는 역할은 v1, v2이다.
Decomposition (3) Dimension-wise Scaling
마지막 연산은 차원(dimension)로 곱하는 과정이다.

첫 번째와 두 번째 선형결합(linear combination)의 계수 [2, 1]를 해당 고유값에 각각 곱하면 오른쪽과 같이 나타나게 된다.
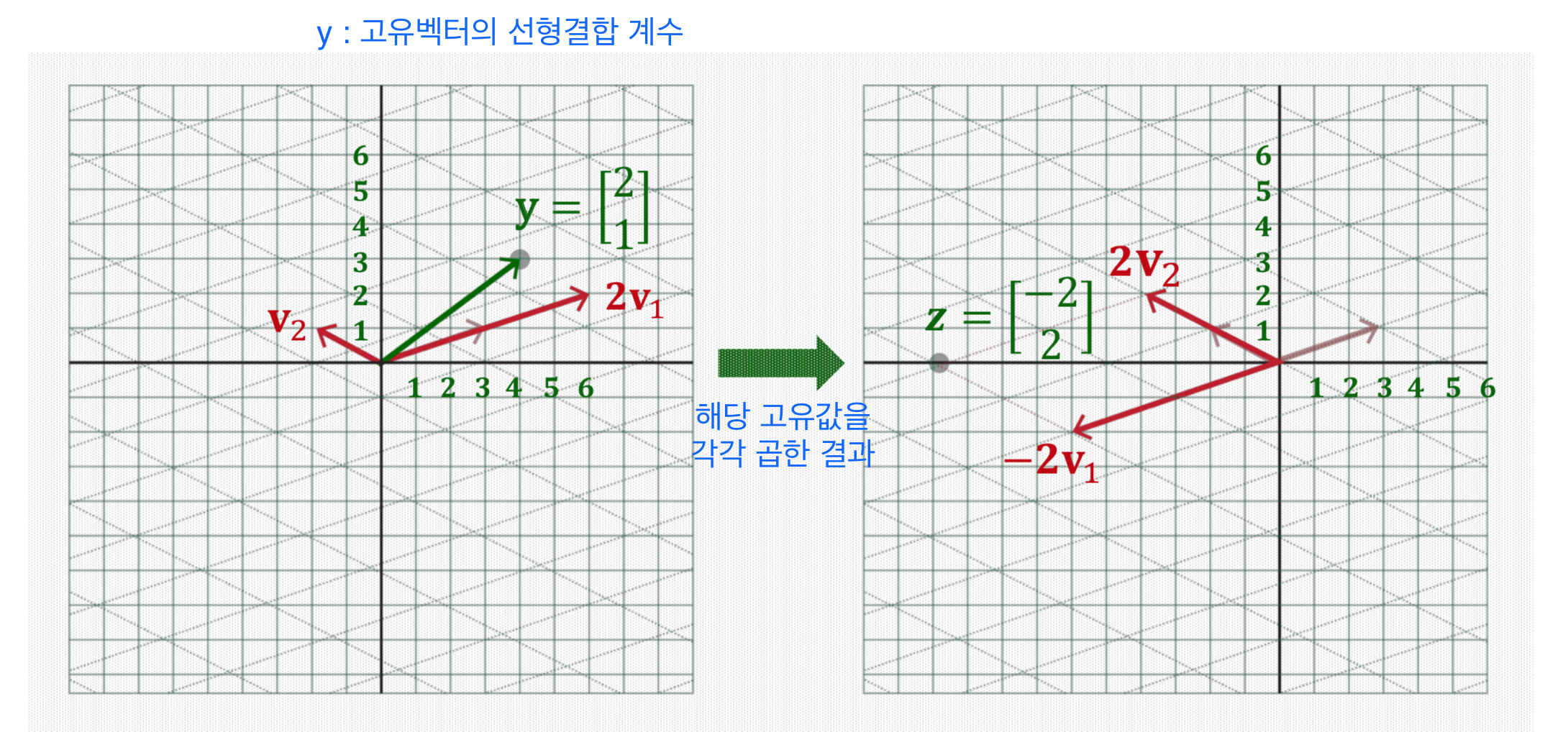
(4) Back to Original Basis
V 는 두 개의 고유벡터로 이루어진 행렬이다.
𝑇(x) = 𝑉(𝐷y) = [v1, v2] * [-2, 2] = -2[v1] + 2[v2]
파란색 계산 과정은 원래 기저 벡터로 복원해주는 과정이다. v1, v2의 해당 계수를 곱해서 선형결합을 만들어 선형결합을 만든 뒤 직교좌표계로 다시 돌아온다.

Overview Transformation using Eigendecomposition

세 가지 과정으로 한다는 것은
- x를 𝑉역행렬하여 고유벡터를 기저로 하는 새로운 좌표 y를 구하는 것이다.
- 그 다음으로 element별로 따로 계산이 간편하게 scaling 한다.
- 마지막으로 원래 좌표계로 다시 복원을 하여 해당 기저벡터로 쓰였던 것들을 다시 적용해서 선형 결합(linear combination) 하는 과정이다.
Linear Transformation via A^(k)

A의 k승을 생각해보면, A는 3x3 매트릭스이며 k=10일 때 10번의 동일한 곱을 하는 과정이다. 회전이동일 경우, 30도를 10번 돌리게 되면 총 300도를 이동하게 된다.
이 과정을 고유벡터를 기저로 하는 space로 갔다가 대각화 행렬 또는 element별로 따로 곱해서 다시 돌아오는 게 𝐴를 곱하는 한번의 과정이였다. 이를 간단하게 하면, 갔다가 diagonal scaling을 하고 다시 돌아오고, 다시 두번째를 곱하고 ... 10번을 반복하게 되면 10번을 다 하는 게 아니라 처음과 끝을 하고 ... 하는 과정이 반복된다.

이 과정을 살펴보면, 𝑉와 𝑉의 역행렬을 곱하면 단위행렬(identity matrix)로 사라지며 가운데가 연결고리처럼 사라지게 된다. 𝐷^(k)는 고유값을 대각화 요소로 가지는 매트릭스인 경우, 계속 곱하게 되면 요소별로 k승을 하는 거랑 같다.
이렇게 계산을 하면 연속적으로 거듭 곱해야하는 연산을 빠르게 계산할 수 있다.
'20. 인공지능과 딥러닝' 카테고리의 다른 글
| [세미나] AI Summit 2019 (0) | 2019.11.29 |
|---|---|
| [인공지능을 위한 선형대수] 선형대수 개념 (0) | 2019.11.17 |
| [인공지능을 위한 선형대수] 대각화 (0) | 2019.10.20 |
| [인공지능을 위한 선형대수] 특성 방정식 (0) | 2019.10.19 |
| [인공지능을 위한 선형대수] 영공간과 직교여공간 (0) | 2019.10.06 |



댓글