edwith의 <파이토치로 시작하는 딥러닝 기초>의 'Lab-05 Logistic Regression' 강의를 정리하였습니다.
[LECTURE] Lab-05 Logistic Regression : edwith
학습목표 로지스틱 회귀(Logistic Regression)에 대해 알아본다. 핵심키워드 로지스틱 회귀(Logistic Regression) 가설(Hypothesis) 손실함수(C... - tkddyd
www.edwith.org
Logistic Regression
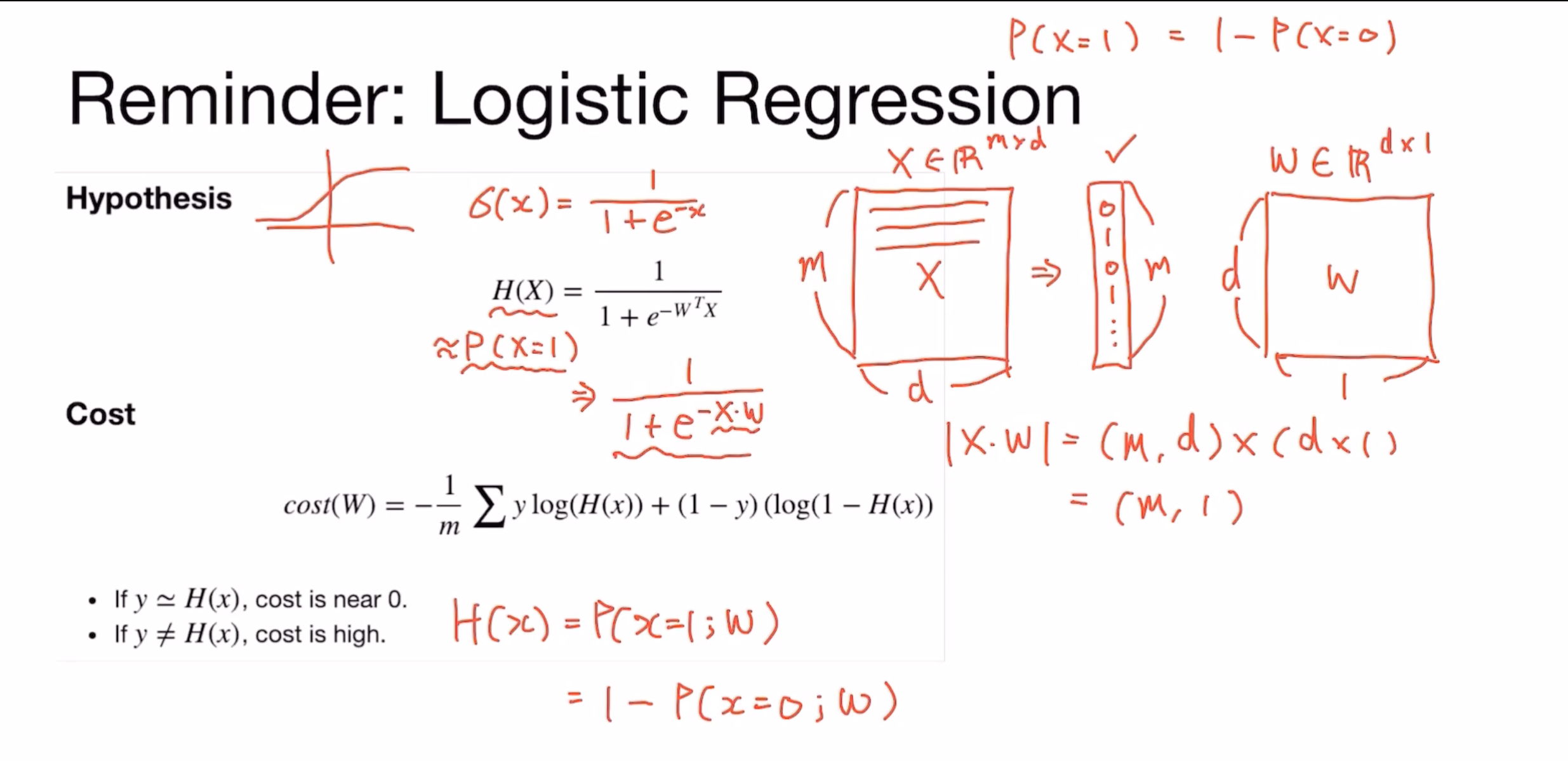
- X라는 데이터는 m개의 데이터들이 d 차원(d 사이즈)의 벡터
=> m이 '0' 또는 '1'로 이루어진 매트릭스
=> m * d 차원의 매트릭스 - 로지스틱 회귀는 d 차원의 1d 벡터가 주어졌을 때, '0' 또는 '1'에 가까운지 찾는 문제
- w (weight 파라미터)는 (d * 1) 차원의 매트릭스
- P(x = 1) = 1 - P(x = 0) : '1'일 확률은 1 - '0'이 될 확률과 같음
- | X * w | = (m * d) x (d * 1) = (m * 1) : m개의 element를 가진 1d 벡터가 됨
sigmoid 함수
- 마이너스 무한대는 '0', 플러스 무한대는 '1'에 가까운 값을 갖게 해주는 함수
Weight Update via Gradient Descent

- weight를 미분한 값에서 learning rate를 곱한 값을 W에서 뺀 뒤, gradient descent가 최소화하는 방향으로 학습하게 됨
Optional: High-level Implementation with nn.Module
class BinaryClassifier(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(8, 1) #self.linear = {w,b}
self.sigmoid = nn.Sigmoid()
def forward(self, x):
return self.sigmoid(self.linear(x))model = BinaryClassifier()# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=1)
nb_epochs = 100
for epoch in range(nb_epochs + 1):
# H(x) 계산 => P(x=1)
hypothesis = model(x_train)
# cost 계산
cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 10 == 0:
prediction = hypothesis >= torch.FloatTensor([0.5])
correct_prediction = prediction.float() == y_train
accuracy = correct_prediction.sum().item() / len(correct_prediction)
print('Epoch {:4d}/{} Cost: {:.6f} Accuracy {:2.2f}%'.format(
epoch, nb_epochs, cost.item(), accuracy * 100,
))
Logistic Classification 개념 설명 (모두를 위한 딥러닝 - 김성훈 교수님 강의)
1. Logistic Classification 가설 함수 정의
2. Coss Function 강의
'20. 인공지능과 딥러닝' 카테고리의 다른 글
| [PyTorch로 시작하는 딥러닝 기초] 09-4 Batch-Normalization (0) | 2020.02.09 |
|---|---|
| [PyTorch로 시작하는 딥러닝 기초] 08. Perceptron (0) | 2020.02.08 |
| [PyTorch로 시작하는 딥러닝 기초] 04-2. Loading Data (0) | 2020.02.02 |
| [세미나] AI Summit 2019 (0) | 2019.11.29 |
| [인공지능을 위한 선형대수] 선형대수 개념 (0) | 2019.11.17 |



댓글