KAIST 산업및시스템공학과 문일철 교수님의 인공지능 및 기계학습 개론 II 중 <10.8 Understand the LDA(Latent Dirichlet Allocation)> 강의를 위주로 기타 자료를 참고하여 정리하였습니다. 잘못된 부분이 있으면 말씀해 주세요.
Topic Modeling
LDA 모델은 주요 키워드를 스스로 선별하는 것이 핵심이며, 문서 모델링에서 적합하게 차원을 축소하는 방법 중 하나이다.
아래 그림은 오바마를 다룬 신문을 모두 수집 후 LDA 모델을 이용하여 토픽을 뽑은 것으로, 전체 내용의 비율을 100이라고 했을 때, 각 토픽의 비중(propotion)이 얼마만큼 다뤄졌는지 나타내는 그래프이다.

알 수 없는 대용량의 문서를 토픽모델링에 적용하여 나온 결과로 주제를 추측할 수 있다. LDA는 소프트 클러스터링이며, 하나의 주제를 하나의 클러스터로 볼 수 있다.
LDA 모델 결과에서 아래의 세 가지 정보를 얻을 수 있다. 따라서 문서를 모두 읽지 않고도, 추출된 토픽 키워드를 바탕으로 문서군의 내용을 대략적으로 파악할 수 있다.
- 토픽
- 토픽의 비중
- 토픽의 단어군
잠재적 디리클레 할당(Latent Dirichlet Allocation, LDA) 모델
아래 그림은 ratsgo 블로그에서 LDA 모델 아키텍처를 plate notation으로 표현한 것입니다. 강의에서 다루지 않은 파라미터별 관념적 의미를 이해하기 쉽게 설명해 주어서 인용하였습니다. 강의자료에서 사용하는 파라미터와 다른 부분(e.g., D -> M)이 있으니 참고 바랍니다.
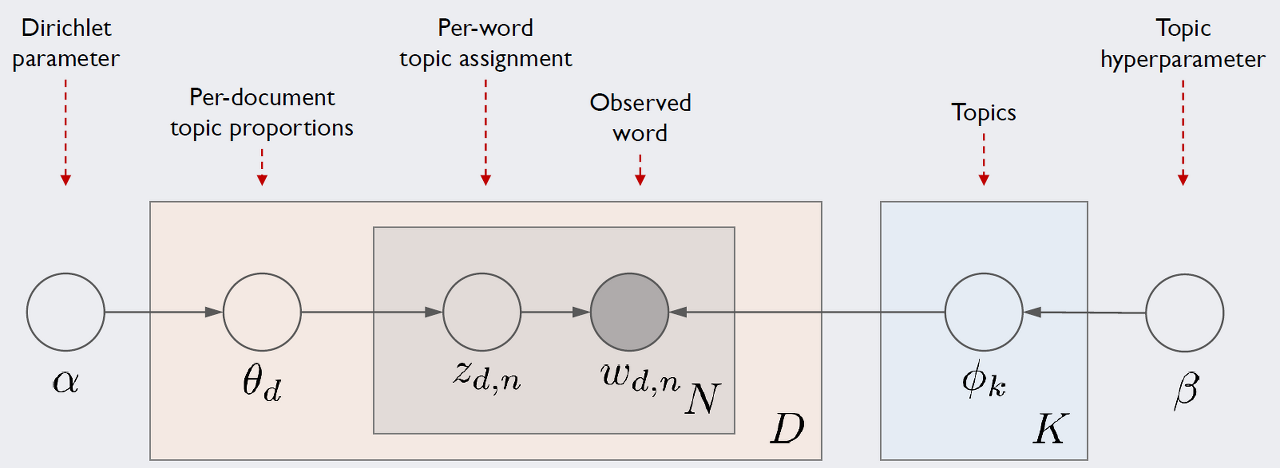
LDA의 아키텍처, 즉 LDA가 가정하는 문서생성과정은 다음과 같습니다. D는 말뭉치 전체 문서 개수, K는 전체 토픽 수(하이퍼 파라메터), N은 d번째 문서의 단어 수를 의미합니다. 네모칸은 해당 횟수만큼 반복하라는 의미이며 동그라미는 변수를 가리킵니다. 화살표가 시작되는 변수는 조건, 화살표가 향하는 변수는 결과에 해당하는 변수입니다.
우리가 관찰 가능한 변수는 d번째 문서에 등장한 n번째 단어 w_d,n이 유일합니다(음영 표시). 우리는 이 정보만을 가지고 하이퍼파라메터(사용자 지정) α,β를 제외한 모든 잠재 변수를 추정해야 합니다. 앞으로 이 글에서는 이 그림을 기준으로 설명할 예정이기 때문에 잘 기억해두시면 좋을 것 같습니다.
출처 : ratsgo 블로그- Topic Modeling, LDA (https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/06/01/LDA/)

- w : 관측되어 있는 변수로, 말뭉치 내 단어를 뜻함
- 단어에 대한 클러스터 어사인먼트 -> z를 통해서 이루어짐
- z : 단어별 Topic assignment (이하, TA) (per-word topic assignment, d번째 문서의 n번째 단어가 토픽 k로 할당될 확률)
- Gaussian Mixture Model (GMM)과 동일하다. (= w에 대한 z 어사인먼트)
- θ : 문서에 대한 TA (per-document topic proportions, d번째 문서가 토픽 k을 차지하는 비율)
- M : 문서 수의 iteration (=말뭉치 전체 문서 개수)
- N : 문서 d에서 등장한 단어 개수
- 문서 TA(θ)와 단어 TA(z)는 multimornial dstribution으로 되어 있음
- α : multinormial distribution에 적용된 θ에 Dirichlet distribution prior가 적용된 형태
- β : φ의 prior로 적용됨
- φ : 토픽의 개수로, 단어가 등장할 확률 (per-corpus topic distributions, 말뭉치 k의 토픽 분포)
LDA 모델은 텍스트 데이터에 대한 소프트 클러스터링(fuzzy clustering, 각 객체가 특정 클러스터에 속하는 정도, 0~1)이다. 반대로, 하드 클러스터링은 포함 여부(0 or 1)를 의미한다. 텍스트 corpus에 대한 구조(structure)를 베이지안 네트워크로 표현하고 있다.

- Prior가 있을 때, 어떤 토픽에서 어떤 단어가 나타날 확률을 결정하는 φ와 합쳐서
- multi-normial distribution을 표현함
- 도큐먼트 레벨의 distribution θ이 단어 레벨의 TA z를 만듦
- 단어 레벨의 TA인 z를 합쳐 φ와 w를 관측할 수 있음
Finding Topic Assignment per Wrod

Generative Proces

(1) Draw each per-corpus topic distributions ϕk~Dir(β) for k∈{1,2,…K}
(2) For each document, Draw per-document topic proportions θd~Dir(α)
(3) For each document and each word, Draw per-word topic assignment zd,n~Multi(θd)
(4) For each document and each word, Draw observed word wd,n~Mult
- α는 전체 코퍼스의 TA을 가지고 있는 것을 기준으로, 어떤 특정 문서를 prior 확률적으로 어사인
- 도큐먼트 레벨의 TA인 θ가 생성됨
- θ는 z의 개별 단어 레벨의 TA에 영향을 줌
- z는 특정 소프트클러스터에 대해서 선택이 된 형태로 z가 생성이 됨
- φ는 β에서 다시 생성이 되는데, 사전 지식이 φ를 만드는 데 영향을 줌
(예; 10개의 토픽이 있을 때, 어떤 토픽에 몇 번 어떤 확률로 나올지에 대한 매트릭 정보) - φ에 특정 단어에 대한 토픽 어사인먼트 정보를 가지고 φ의 확률을 가져와, multi-normial distribution에서 파라미터에서 하나의 단어를 선정하겠음 ->그래서 한 단어가 쓰여짐
- 1,000개의 문서가 이 모든 과정을 반복함 -> 제너러티브 프로세스를 읽는 방식
- A word w is generated from the distribution of φ_z word-topic distribution
- 단어 w : φ_z(φ와 z가 합쳐짐)의 distribution에서 하나로 선택되어 나옴
- z topic is generated from the distribution of θ document-topic distribution
- 토픽 z : 도큐먼트 레벨의 θ 토픽 디스트리뷰션에서 나옴
- θ document topic distribution is generated from the distribution of α
- 도큐먼트 토픽 θ : 코퍼스 레벨의 α에서 나옴
- φ word-topic distribution is generated from the distribution of β
- φ 단어-토픽 디스트리뷰션 : 개별 단어들이 얼마나 자주 쓰이는지에 대한 사전 지식에서 나옴
- •If we have Z distribution, we can find the most likely θ and φ
- •θ: Topic distribution in a document
- •φ: Word distribution in a topic
- •Finding the most likely allocation of Z is the key of inference on θ and φ
•w는 관측 데이터이기 때문에 바뀔 일이 없으며, α와 β는 사전 지식이므로 고정이다.
•Floating한 z, θ, φ 파라미터는 잘 어사인 해보자
•α와 z를 알고 있기 때문에 θ를 측정할 수 있음
•z를 알아내는 게 핵심이며, z-distribution을 알면 θ와 φ를 알아낼 수 있음
➡ θ와 φ를 알면 도큐먼트의 topic distribution이므로, 주어진 코퍼스에서 토픽이 얼마만큼의 비율(porption)로 존재하는지 알 수 있다.
Gibbs Sampling
결합 사후 분포 p(θ1,θ2,θ3|D)에서 샘플을 추출하기 어렵기 때문에, 모든 조건부 사후 확률 분포(p(θ1|θ2,θ3,D), p(θ2|θ1,θ3,D), p(θ3|θ1,θ2,D))에서 샘플을 추출하여 사후 분포를 계산한다.
LDA 모델에서는 Collapsed Gibbs Sampling 방법을 이용하여 z를 구한다. 이 방법에서는 구하고자 하는 변수(zi) 외 나머지(z-i)는 모두 고정한 뒤, 불필요한 일부 변수는 샘플링에서 제외한다.
우리가 구하고자하는 i번째 단어에 어떤 토픽이 할당되어 있는지를 의미하는 z_i를 추정할 때, z_i 외 나머지 변수는 z_(-i)는 모두 고정되어 있다고 가정한다. w와 z_(-i)가 주어졌을 때, z_i 값을 샘플링한다.

위 그림에서는 z_1, z_2, z_3 순서대로 값을 고정시키면서 샘플링하는 것을 의미한다.

z_(−i)와 w가 주어졌을 때, d번째 문서의 i번 째 단어의 토픽이 j일 확률을 의미한다.
zi 값을 구했던 것처럼 모든 단어마다 깁스 샘플링을 적용하여 단어에 토픽을 할당하면 ϕ와 θ 값을 구할 수 있다. 초기 파라미터는 랜덤값으로 설정하여, 모든 단어에 동일한 과정을 반복한다. 이 과정을 무수히 반복하면 특정 값에 수렴하여 우리가 기대하는 결과를 얻을 수 있다.

Collapsed Gibbs Sampling에서 반복 횟수를 증가할 수록 파라미터가 수렴하는 것을 확인할 수 있다.
LDA 모델에서 깁스 샘플링을 구하는 자세한 과정은 아래 아티클에서 자세히 설명하고 있습니다.
Topic modeling using Latent Dirichlet Allocation(LDA) and Gibbs Sampling explained!
How Topic Modelling works and how to implement it using LDA and Gibbs Sampling
medium.com
토픽의 개수 최적화
우리가 지정해야하는 파라미터인 토픽의 개수 k는 Perplexity 지표를 통해서 최적의 개수를 찾을 수 있다. 또한, pyLDAvis 라이브러리를 이용하여, LDA 모델 분석 결과인 토픽별 단어의 연관성과 문서 내 토픽 비중을 시각화할 수 있다. 최적화한 k의 개수를 육안으로 해석할 수 있다.

참고 자료
인공지능 및 기계학습 개론 II 강좌소개 : edwith
본 강의는 '인공지능 및 기계학습 개론 1' 를 이어 제공되는 강의로 기계 학습에 대한 이론적 지식을 확률, 통계, 최적화를 바탕으로 소개합니다. 이 과정에서 다양한 확률 이론 및... - KAIST 산업
www.edwith.org
Topic Modeling, LDA · ratsgo's blog
이번 글에서는 말뭉치로부터 토픽을 추출하는 토픽모델링(Topic Modeling) 기법 가운데 하나인 잠재디리클레할당(Latent Dirichlet Allocation, LDA)에 대해 살펴보도록 하겠습니다. 이번 글 역시 고려대 강
ratsgo.github.io
LDA 파라미터 추정: 깁스 샘플링을 써서
이런 걸 써봐야 누가 읽겠어 했던 글이 의외로 블로그의 트래픽을 먹여살리고 있다. 4년 전에 쓴 LDA(Latent Dirichlet Allocation): 겉핥기는 지금까지도 꾸준히 조회수 탑을 달리는 스테디포스트가 되었
4four.us
'20. 인공지능과 딥러닝' 카테고리의 다른 글
| 2023 Google I/O : 인공지능, 검색엔진, 하드웨어 (0) | 2023.05.17 |
|---|---|
| 오토인코더의 모든 것 (1/3) 03. Autoencoders (1) | 2022.03.26 |
| Asynchronous Methods for Deep Reinforcement Learning (A3C) (0) | 2020.09.14 |
| DQN 실습 :: CartPole 게임 (1) | 2020.08.30 |
| 스터디 | Playing Atari with Deep Reinforcement Learning (0) | 2020.08.09 |




댓글