Least Squares와 그 기하학적 의미
Least Square Problem

위 방정식에서 해(solution)이 없는 이유는 벡터 𝐴의 span인 Col 𝐴 를 𝐛 벡터가 포함되지 않기 때문이다. 오류를 최소로 만드는 해를 찾는 게 최소제곱법(Least Square)이다. 다시 풀어서 설명하면 주어진 Colum space 𝐴에 있을 수밖에 없는 어떤 점에서 𝐛 라는 벡터와 가장 가까운 벡터 𝐱 를 찾는 문제이다.
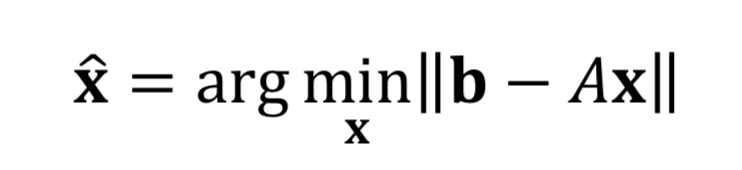

위의 그림을 보면, 𝐛 는 Col 𝐴 밖에 있기 때문에 해가 없지만, Col 𝐴 평면에서 𝐛 랑 가장 가까울 수 있는 점을 찾는 게 목표이다. 𝐴 와 그 지점에 해당하는 linear coefficent를 찾으면 𝐛 hat이 되며, 𝐛 hat은 최단거리가 된다.
Geometric Interpretation of Least Squares
𝐛 와 𝐛 hat이 가장 가깝다는 것은, 𝐴𝐱의 한 점과 𝐛 의 길이가 최단거리가 되는 점을 뜻한다. 아래 그림의 파란색 점선이 최단거리가 되기 위해서는 𝐛 와 𝐛 hat, Col 𝐴이 수직이 되어야 한다. 𝐴𝐱(실선)를 랜덤으로 잡았을 때에도 직교해야지 최단거리가 된다.
평면 위에 있는 모든 점과 수직이 되어야 최단거리가 된다
𝐛 hat과 𝐛 hat의 선형변환으로 만들어낸 𝐱 hat을 찾고자 하는 것이 미션이다. 즉, 평면 내 모든 벡터와 수직이어야 한다.
𝐴𝐱 = x1*a1 + x2*a2 + x3*a3 라고 할 때, x1, x2, x3에 아무 값을 넣어도 Col 𝐴 에 있는 한 벡터가 된다. 어떤 벡터든지 벡터 𝐛와 수직이 되어야 한다.

(𝐛 - 𝐛 hat) ㅗ (a1*x1 + a2*x2 + a3*x3) = 0
재료 벡터로 쓰이는 a1, a2, a3 와 𝐛 - 𝐛 hat 과 수직이라면, 𝐛 - 𝐛 hat은 항상 수직이 된다.
Normal Equation (정규 방정식)

a1, a2, am 벡터와 (𝐛 - 𝐛 hat)이 직교하다는 것을 내적으로 바꾼 후, a 벡터를 전치(transpose) 하면 '0'이 된다. 이는 다시 a1, a2, am 벡터를 메트릭로 표현하면 정규 방정식 (Normal Equation)이 된다.
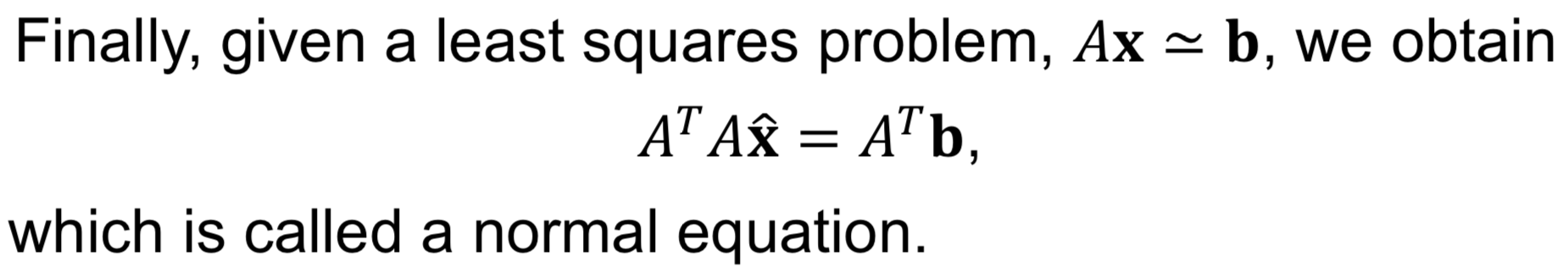
정규 방정식은 신경망에서 비용함수(cost fucntion)의 최소값을 구하기 위한 과정 arg min J(θ) 에서도 언급된다.
'20. 인공지능과 딥러닝' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 특성 방정식 (0) | 2019.10.19 |
|---|---|
| [인공지능을 위한 선형대수] 영공간과 직교여공간 (0) | 2019.10.06 |
| [인공지능을 위한 선형대수] Least Squares Problem(최소자승법) 소개 (0) | 2019.09.24 |
| [인공지능을 위한 선형대수] 전사함수와 일대일함수(단사함수) (0) | 2019.09.07 |
| [인공지능을 위한 선형대수] 선형 변환 (Linear Transformation) (0) | 2019.09.07 |




댓글