[인공지능을 위한 선형대수] Least Squares Problem(최소자승법) 소개

이 글은 주재걸 교수님의 <인공지능을 위한 선형대수 - Least Squares Problem 소개> 강의를 정리하였습니다.

---

Least Squares Problem (최소 자승법) 

Over-determined Linear Systems (#equations >> #variables)

변수가 방정식 보다 많은 경우, over-determined 선형 시스템이라고 한다. 이 경우, 해(solution)이 존재하지 않는다. (e.g., 100개의 방정식을 단 3개의 변수만으로 만족하는 해를 찾기 어렵다.)

 

방정식이 많아질 수록 b 벡터의 span 안에 모두 포함될 확률이 굉장히 희박해진다. 

즉, 해가 존재한다는 것은 위 선형 시스템에서 방정식이 100개까지 증가한다고 가정할 때, 상수 벡터인 b 벡터 [66, 74, 78, ... ]가 100차원의 span 안에 있어야 한다. 광할한 공간인 100 차원이 3개의 벡터(x1, x2, x3) 안에 쏙 들어와야 한다는 것이다(?)

 

해가 존재하지 않더라도, 근사적으로 해를 구해보는 게 최소자승법의 가장 기본적인 아이디어이다. 그렇다면 수학적으로 가장 근사한 해(best approximate solution)가 무엇인지와 그와 관련된 개념들을 살펴보도록 하자.

 

1. Inner Product (내적)

내적의 정의는 벡터마다 요소들을 모두 곱해서 더한 값이다. 내적을 행렬의 곱의 관점에서 살펴보면 다음과 같다. 𝐮 벡터를 변환하여 𝐮𝑇 으로 만든 뒤 𝐯 를 곱하게 되면 1 x 1 스칼라 값이 나오게 된다.

 

벡터의 곱으로 살펴본 내적의 정의  

 

내적의 특징

내적은 a) 교환 법칙, b) 분배 법책이 성립된다. c) '0' 보다 크거나 같은 자기 자신의 내적을 구했을 때, '0'이 되려면 그 벡터는 '0' 일 때에만 성립된다. 교환법칙과 분배법칙을 일반화하면 (𝑐 𝐮 +⋯+𝑐 𝐮 )∙𝐰=𝑐 (𝐮 ∙𝐰)+⋯+𝑐 (𝐮 ∙𝐰) 으로 표현할 수 있다. 따라서 내적 후에 선형결합을 한 것과 선형결합 후 내적을 한 것과 값은 같다.

 

2. Vector Norm (벡터 노름)

벡터 노름은  벡터의 길이를 뜻한다. 𝐯 의 길이 또는 norm은 항상 '0' 보다 크거나 같아야 하며 (non-negative), 더블바 ' || '으로 표현한다. 자기 자신과의 내적으로도 정의할 수 있다. 

Vector Norm 정의

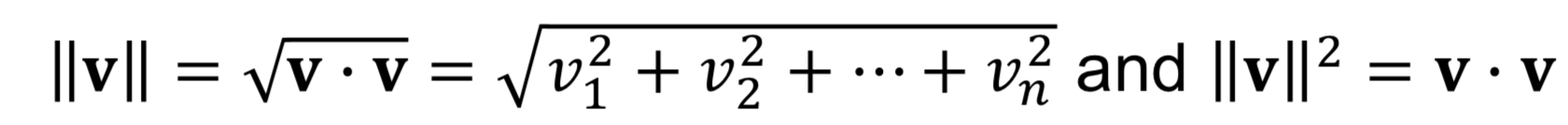
Geometric Meaning of Vector Norm

상수배를 하면 벡터의 길이는 상수배만큼 증가한다. 길이이기 때문에 스칼라𝑐 에도 절대값이 붙게 된다.

노름(norm)에 상새부를 곱하면 길이도 상수의 절대값만큼 증가한다. 

3. Unit Vector (단위벡터)

벡터 길이를 '1'로 만드는 과정을 normalizing 이며, 그 벡터를 unit vector 라고 한다. 벡터의 길이를 오리지널 벡터에 나누면 단위벡터가 된다.

벡터 Normalizing 정의

2차원으로 살펴본 단위벡터

 

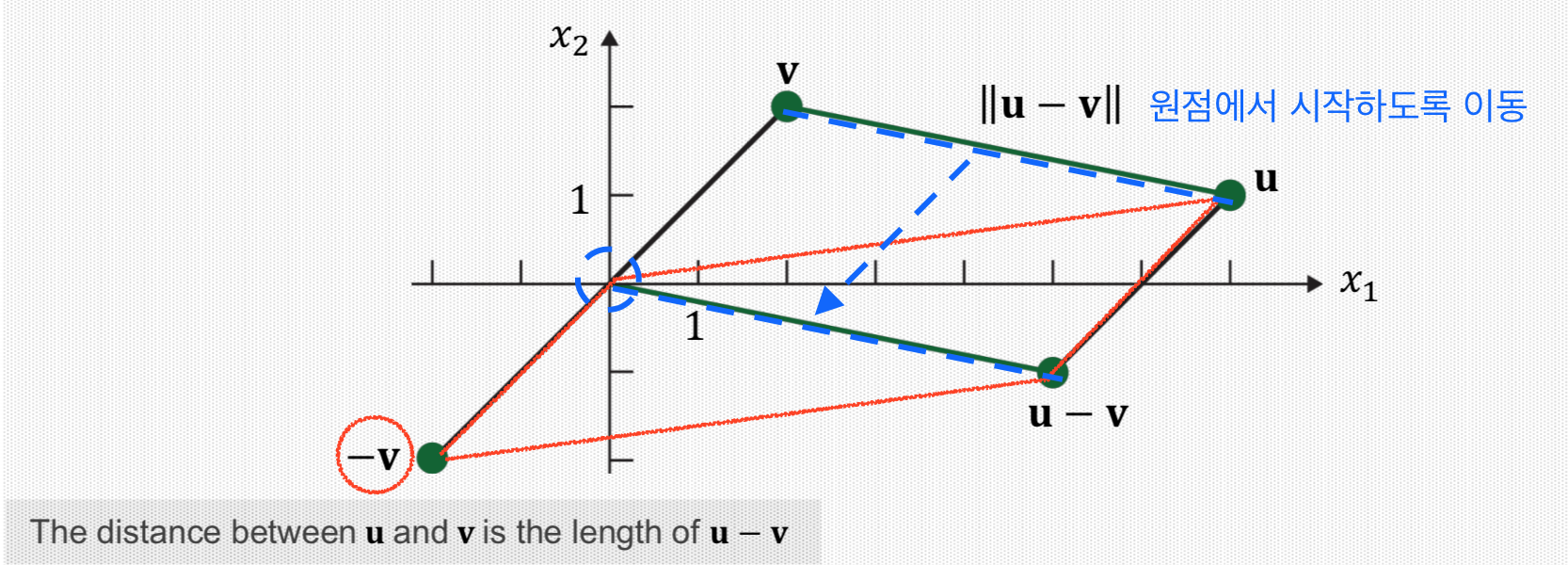
4. Distance between Vectors

벡터간의 거리는 벡터의 길이(norm)을 활용하여 정의할 수 있다. 두 벡터 (𝐮, 𝐯) 간의 차이를 구한 후, 벡터의 길이를 구하게 되면 벡터간의 거리가 된다.

두 벡터 (𝐮, 𝐯)간의 거리는 norm을 활용하여 계산할 수 있다.

 

차이 벡터를 구한다는 것은 1*𝐮 + (-1)*𝐯 으로 변형하여 살펴보면, 원점에서 출발한 𝐮-𝐯 벡터의 길이를 계산하면 된다.

원점으로 이동시킨 후 차이벡터를 구한다. 

5. Inner Product and Angle Between Vectors

내적을 이용하여 두 벡터의 각도를 구할 수 있다. 각각의 벡터의 길이를 구한 후, 코사인(cosine)을 곱하면 두 벡터의 내적 값과 같다.

내적을 통해서 두 벡터의 각도를 구할 수 있다. 

 

6. Orthogonal Vectors (직교 벡터)

두 벡터가 수직(90도)인 경우, 코사인 값은 '0'이 되기 때문에 두 벡터의 내적도 '0'이 된다. 따라서 두 벡터를 내적한 값이 '0'일 경우에도 각도가 90도라는 것을 알 수 있다.

Orthogonal Vectors 정의

 

Least Squares: Best Approximation Criterion  

 

세 개만으로 만족하는 해를 가지고 네 개의 방적식에 해를 대입하면 네 번째 방정식은 만족하지 않고 오류(b - Ax)가 발생한다. 그 결과, 해가 얼마큼 틀렸는지 파악할 수 있다. 

 

정량적으로, 위의 방정식 해가 더 적은 오류(9.55)를 내기 때문에 더 나은 결과라고 판단할 수 있다. 이처럼 오류를 최소화하는 해를 찾는 목적이 최소제곱법(Least Square Problem)이다. 이를 위해서는 첫 번째로 목적함수(𝐛−𝐴𝐱)를 명확하게 정의해야 하며, 두 번째로 ||𝐛−𝐴𝐱||를 최소로 만드는값(argmin)을 x hat 으로 한다.

 

Least Square Problem 정의